Nonlocal Lagrangian
In field theory, a nonlocal Lagrangian is a Lagrangian, a type of functional ![\mathcal{L}[\phi(x)]](/2012-wikipedia_en_all_nopic_01_2012/I/38e8e67ef381b989541abc22a94654c4.png) which contains terms which are nonlocal in the fields
which contains terms which are nonlocal in the fields 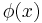 i.e. which are not polynomials or functions of the fields or their derivatives evaluated at a single point in the space of dynamical parameters (eg. space-time). Examples of such nonlocal Lagrangians might be
i.e. which are not polynomials or functions of the fields or their derivatives evaluated at a single point in the space of dynamical parameters (eg. space-time). Examples of such nonlocal Lagrangians might be
Actions obtained from nonlocal Lagrangians are called nonlocal actions. The actions appearing in the fundamental theories of physics, such as the Standard Model, are local actions - nonlocal actions play a part in theories which attempt to go beyond the Standard Model, and also appear in some effective field theories. Nonlocalization of a local action is also an essential aspect of some regularization procedures. Noncommutative quantum field theory also gives rise to nonlocal actions.
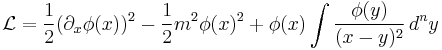
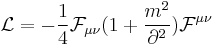
![S=\int dt \, d^dx \left[\psi^*(i\hbar \frac{\partial}{\partial t}%2B\mu)\psi-\frac{\hbar^2}{2m}\nabla \psi^*\cdot \nabla \psi\right]-\frac{1}{2}\int dt \, d^dx \, d^dy \, V(\vec{y}-\vec{x})\psi^*(\vec{x})\psi(\vec{x})\psi^*(\vec{y})\psi(\vec{y})](/2012-wikipedia_en_all_nopic_01_2012/I/67d37bf59762d9161b4cab65fd1ebaec.png)